Introduktion

Johan Radon

Dette materiale er udarbejdet med henblik på at inspirere og hjælpe i en SRP opgave med CT skanning som emne. Vi vil komme ind på hvordan CT skanninger virker, især med fokus på matematikken i CT rekonstruktion. Vi vil beskrive CT problemet med et lineært ligningssystem og komme ind på, hvordan man løser det med mindste kvadraters metode.

Læringsmål

Formålet med dette materiale er at eleven kan:

  1. Forklare hvad vi måler i en CT skanning samt, hvad vi ønsker at rekonstruere.
  2. Opskrive en matematisk model for røntgenabsorption i sammensat materiale baseret på fysik.
  3. Opskrive et simpelt linært ligningssystem baseret på lille CT problem ($2\times 2$ eller $3\times 3$ pixels).
  4. Forklare forskellen på under-, entydigt og over-bestemte systemer, samt hvilke konsekvenser det har for løsningen.
  5. Anvende mindste kvadraters metode til at løse et lille ligningssystem.

Historie

Johan Radon

Det er nok de færreste, der går og tænker over at for godt 50 år siden, eksisterede CT-skannere slet ikke, og mulighederne for at se ind i kroppen uden at åbne op, var ganske begrænsede. Man kunne tage røntgenbilleder, men den slags billeder giver slet ikke den samme detaljegrad som CT. CT er også baseret på absorption af røntgenstråler i materiale, men er en form for udvidelse af de traditionalle røntgenbilleder. Røntgenbilleder adskiller sig fra CT ved faktisk at være et billede "man tager". Altså meget tilsvarende et fotografi, hvor en 3D virkelighed bliver projeceret ned på et 2D billede. I stedet for synligt lys bruger man bare røntgenlys som kan gennemtrænge mange materialer. Nogen kalder også røntgenbilleder for "skyggebilleder", fordi man på en måde ser skygger fra objektets indre struktur. De billeder man får ud efter en CT skanning er ikke billeder "man tager", men derimod en rekonstruktion af et tværsnit, som afhænger af en matematisk model og beregningsmetode. I CT skanninger bruger man kort sagt en lang række "skyggebilleder" taget fra forskellige vinkler til at lave en rekonstruktion af et objekts indre struktur. I dag bruges CT bl.a. til at observere avancerede knoglebrud, sygdom i blødt væv i kroppen og hos tandlægen til at se efter huller. Men CT har ikke kun medicinske andvendelser. CT bruges bl.a. også til at skanne bagage i lufthavnen og i industrien til at kvalitetskontrol af produkter. Fx kan man skanne vindmøllevinger for at tjekke materiale strukturen der har stor betydning for vingens styrke [1].

Røntgenstråler har været kendt siden slutningen af 1800-tallet, hvor de blev opdaget og navngivet efter den tyske fysiker Willhelm Röntgen, der var den første til at systematisk studere strålerne.

Allerede for omkring 100 år siden i 1917 lagde den østrigske matematiker Johann Radon det matematiske grundlag for CT-skanning, som vi kender det i dag. Han studerede projektioner, det at tage et objekt og afbilde det i en lavere dimension, og mulighederne for at rekonstruere objektet, hvis man kender nok projektioner af det. For et simpelt eksempel forestil dig en figur i LEGO, og hvor mange billeder fra forskellige vinkler du ville have brug for, hvis du skulle bygge den igen kun ud fra billederne. Med få billeder kan du måske bygge en figur der ligner i grove træk, men hvis du skal have alle små detaljer med, har du brug for mange billeder. Jo flere billeder du har, jo lettere bliver det at bygge den igen.

Der skulle dog gå lang tid før CT-skannerne kom. Først over 50 år senere i 1971, blev den første praktiske brugbare CT-skanner markedsført. Det var Allan McLeod Cormack og Godfrey Hounsfields fælles indsats op gennem 50'erne og 60'erne, der gjorde maskinen til virkelighed og de modtog for deres arbejde Nobelprisen i Medicin i 1979.

Sidenhen er CT-skannere blevet langt mere sofistikerede, som du også kan se herunder. Hounsfields prototype og den første serie af CT-skannere skannede langs parallelle linier, mens nyere modeller skanner langs en vifte af linier udspringende fra det samme punkt. Det har en række tekniske fordele, som vi ikke vil gå i detaljer med her.

Der findes mange matematiske metoder, der kan bruges til CT rekonstruktion. Filtered backprojection er nok den mest udbredte metode fordi beregningerne er meget hurtige i en computer. Matematikken bag denne metode er dog en smule kompliceret, så den vil vi ikke studerere nærmere i denne øvelse. Vi vil i stedet lave CT rekonstruktion ved at formulere et lineært ligningssystem og løse det vha. mindste kvadraters metode. Denne tilgangsvinkel er også meget udbredt, især hvis man af en eller anden grund har en begrænset mængde data. Det er filtered backprojection nemlig ikke så velegnet til.

Godfrey Hounsfields CT-skanner prototype.
Moderne CT-skanner. Symbolforklaring: T: x-ray rør, D: x-ray detektorer X: x-ray stråler R: Rotationsretning.

Talpuslespil

Lad os starte med at betragte nogle talpuslespil i figur 5 for at varme op til CT problemet.

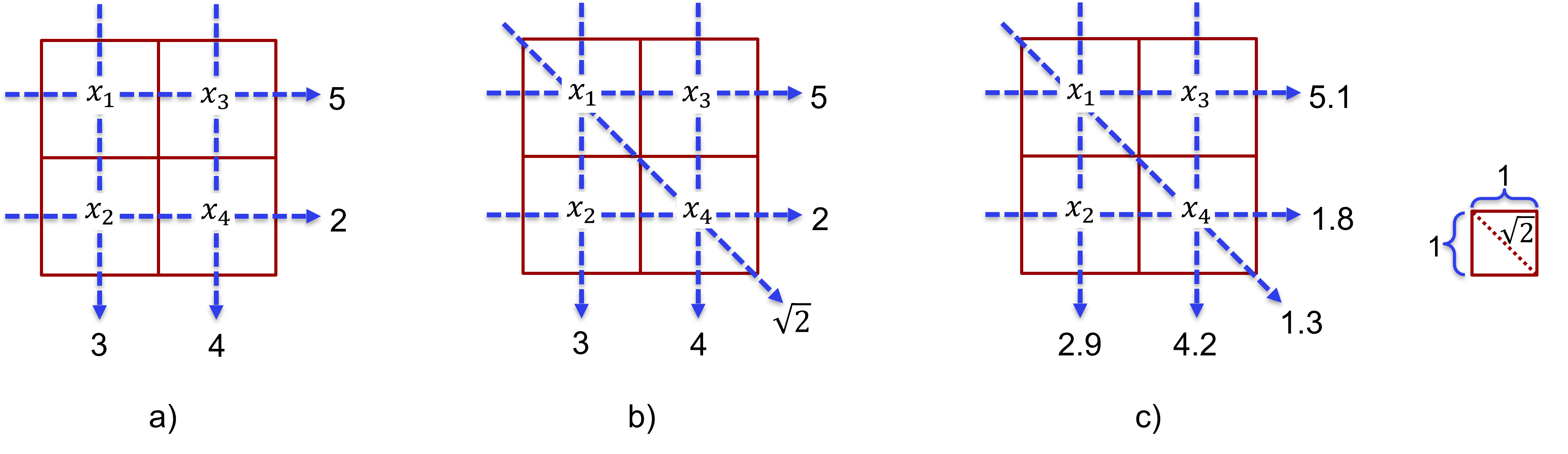
Talpuslespil. Hvad skal $(x_1, x_2, x_3, x_4)$ være for at alle summer langs de blå linjer stemmer? Bemærk, den diagonale sum ganges med $\sqrt{2}$ fordi den diagonale linjes vej gennem hvert pixel er $\sqrt{2}$ gange længere end de lodrette og vandrette linjers vej. a) Dette talpuslespil har uendeligt mange løsninger. b) Dette talpuslespil har én enkelt løsning. c) Dette talpuslespil har ingen løsning.

Vi betragter talpuslespillet i figur 5a). Målet er at udlede værdierne i hvert pixel, sådan at alle summer langs linjerne stemmer overens med "målingerne" for enden af linjerne. Du kan måske finde mere end én løsning der passer? Faktisk er der uendeligt mange løsninger til dette problem! Det vender vi tilbage til når vi snakker om CT senere.

Vi kunne også have et talpuslespil som i figur 5b). Her introducerer vi yderligere en sum langs en diagonal linje. Vi tager højde for at den diagonale linjes vej gennem hvert pixel er $\sqrt{2}$ gange længere end de lodrette og vandrette linjers vej. Nu har talpuslespillet kun en enkelt løsning der stemmer med alle summer. Hvad skete der? Vi introducerede mere information i puslespillet sådan at der nu er tilstrækkeligt med information til at løse det entydigt. Kan du finde løsningen? Senere vender vi tilbage til, hvordan man angriber dette problem på en systematisk, matematisk måde.

I figur 5c) har vi endnu en version af talpuslespillet. Denne gang forestiller vi os at måleudstyret er underlagt usikkerhed, og sådan vil det jo egentlig altid være i den virkelige verden. Men måleusikkerheden har gjort, at der ikke længere findes en løsning til talpuslespillet. I denne situation kunne man vælge den løsning, der er tættest på at løse systemet. Men hvad betyder det? Det vender vi også tilbage til senere i materialet.

Talpuslespil som disse er faktisk fuldstændig ækvivalente til CT problemet, og de tre forskellige situationer ovenfor svarer til alle de udfordringer vi kan møde i CT. I dette materiale vil vi lære at opstille et lineært ligningssystem der beskriver puslespillet/CT problemet, samt hvordan vi løser det, også når vi har udfordinger som ingen eller uendeligt mange løsninger. Vi vil vende tilbage til vores talpuslespil flere gange i materialet for at illustrere nogle at principperne i matematikken bag CT.

CT problemet

CT står for "computed tomography", og ordet tomografi stammer fra de græske ord: 1) Tomos = tværsnit, og 2) Graphos = at beskrive. Det giver måske allerede et lille hint om, hvad CT går ud på.

I CT udnytter vi at forskellige materialer absorberer røntgenstråling i forskellig grad. Kort fortalt: Vi sender røntgenstråler igennem et objekt og observerer forskellen på intensitet før og efter. Hvis vi gør dette fra mange retninger, kan vi sige noget om fordelingen af materiale inde i objektet, fx i et tværsnit.

For at simplificere problemet vil vi i denne øvelse gennemgå matematikken med udgangspunkt i et 2D CT problem. Dvs. vi blot rekonstruerer ét tværsnit af et objekt. Til allersidst vil vi kort sætte nogle ord på, hvordan problemet generaliseres til 3D. Matematikken er ikke anerledes i 3D, men det kan være lidt sværere at forestille sig og visualisere.

Parametre

CT problemet går ud på at rekonstruere et billede. Billedet består af $n=N\times N$ pixels, og vi giver hvert pixel et navn som vist i figur 6. Hvert pixel repræsenterer en såkaldt absorptionskoefficient, og disse er de ubekendte parametre som vi ønsker at rekonstruere. Forskellige materialer har forskellige absorptionskoefficienter, og de angiver i hvor høj grad materialet dæmper røntgenstråling. Et materiale med høj absorptionskoefficient lader ikke meget stråling slippe igennem, og et materiale med absorptionskoefficient 0 lader al stråling passere. Derfor kan vi ved at rekonstruere absorptionskoefficienterne inde i et objekt se kontrast mellem forskellige materialer. Faktisk er absorptionskoefficienterne proportionale med materialets densitet, hvilket kan give os en bedre intuition om hvilke materialer vi ser på i en CT rekonstruktion.

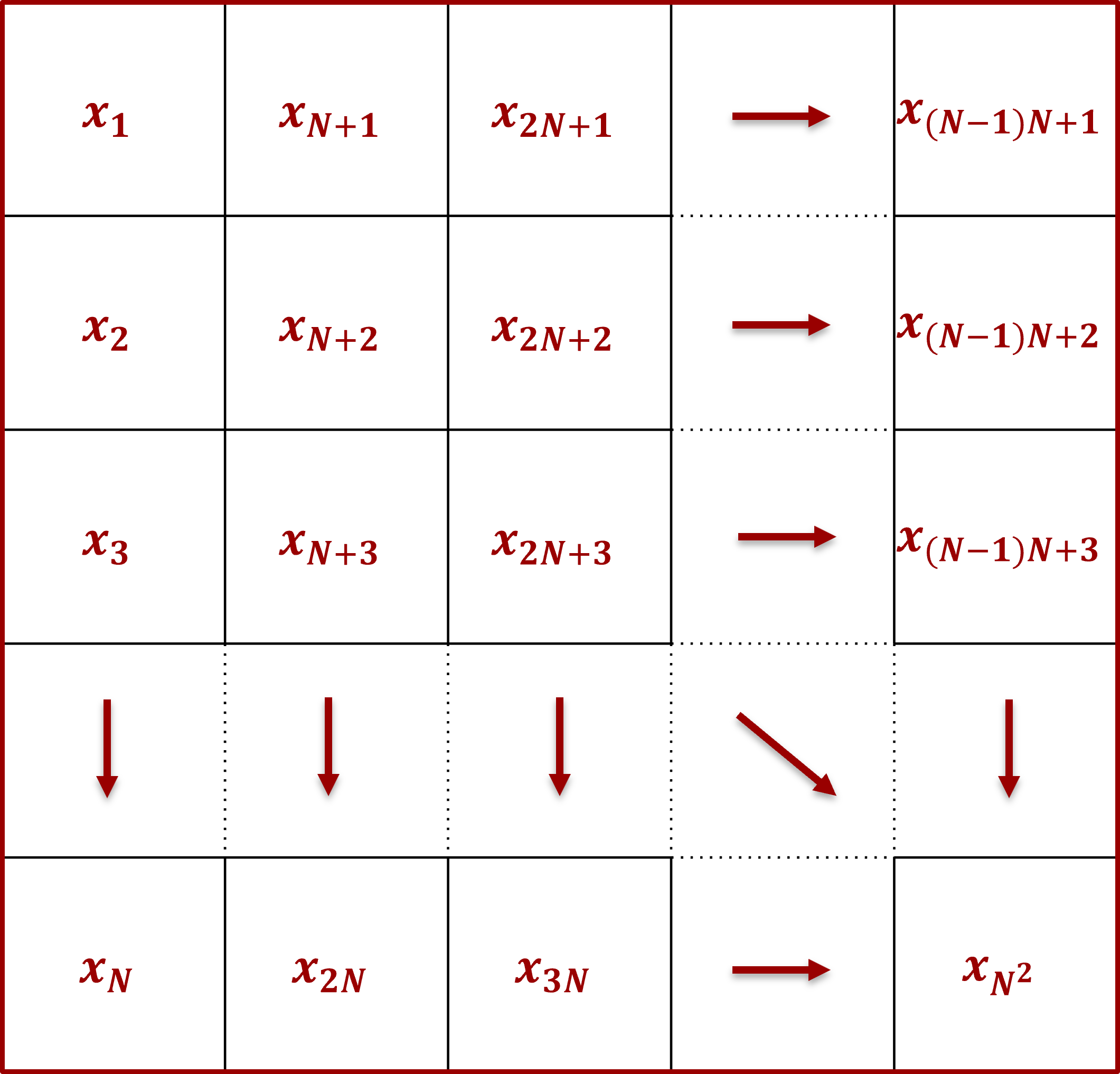
Et billede inddelt i pixels med navne fra $x_1$ til $x_{N^2}$, hvor $N$ angiver antal pixels i en række/kolonne.

Data

I CT sender vi røntgenstråling igennem et objekt og måler intensiteten på den anden side. I 2D CT skal man forestille en flade af røntgenstråler, der bestråler hele objektet fra én side på én gang og detektoren på den anden side vil bestå af en række detektorpixels, som hver optager intensitet. I et mere matematisk sprog kalder vi en sådan måling en projektion, fordi et 2D objekt bliver afbilledet på en 1D flade. Hvis man optager en samling af 1D projektioner fra mange vinkler, vil man kunne lave en 2D rekonstruktion svarende til et tværsnit af objektet igennem den flade røntgenstrålerne belyste. Vi kan igen vende tilbage til talpuslespillet. I figur 7 viser vi, hvordan man kan lave tre 1D projektioner gennem puslespillet.

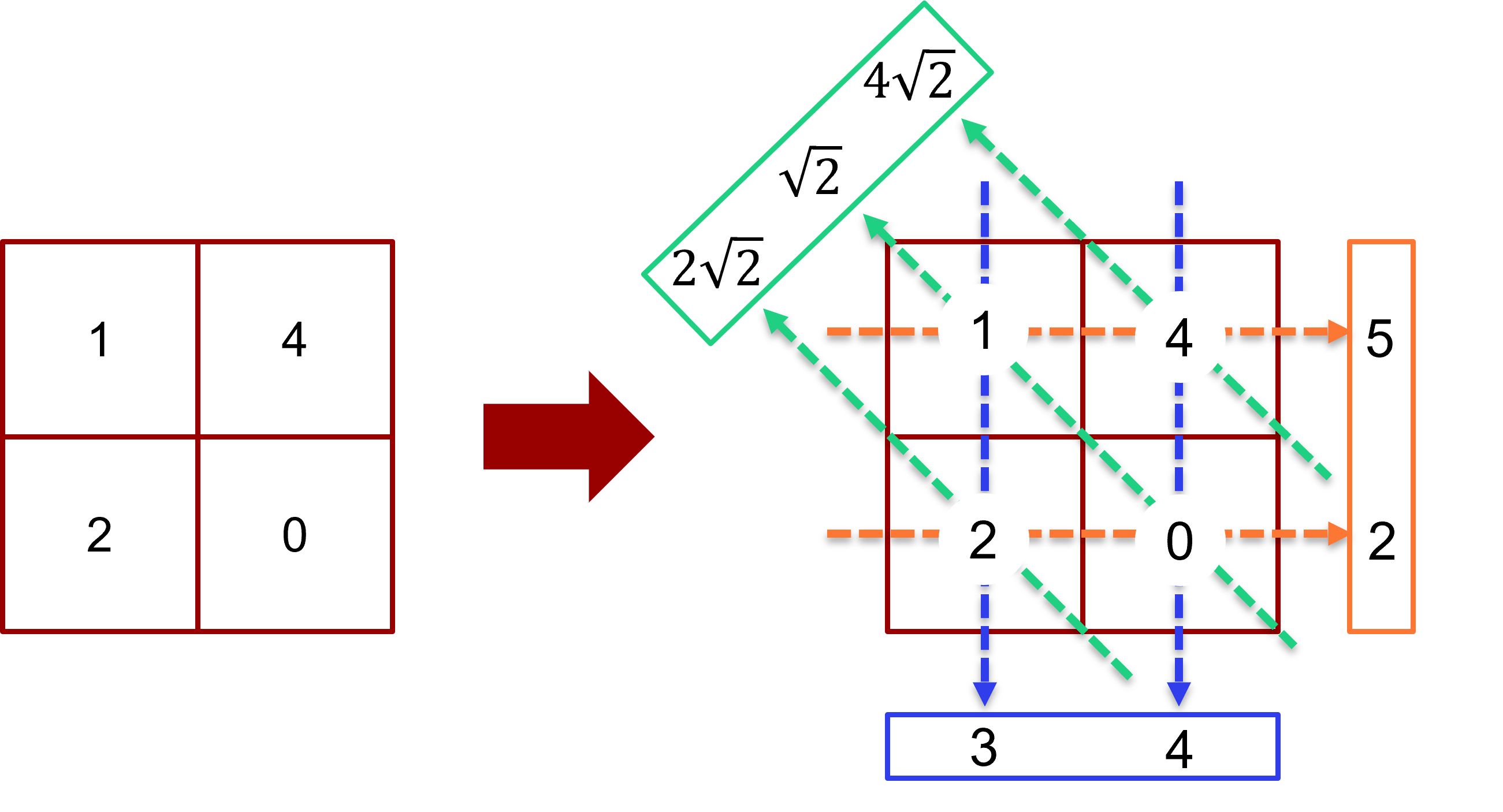
Projektioner gennem talpuslespillet. De blå, grønne og orange bokse angiver hver en 1D projektion gennem 2D objektet.

Når man laver sine CT målinger kan man bruge forskellige bestrålingsgeometrier. De to mest udbredte er parallelle stråler og vifte stråler som illustreret i figur 8. I dette materiale vil vi tage udgangspunkt i den parallelle geometri, fordi det er det simpleste at forestille sig. I praksis vil mange CT-skannere dog måle med viftegeometri fordi en røntgenkilde naturligt udsender stråler i alle retninger, hvilket svarer til en viftegeometri, hvis man måler på en detektor som i figur 8. Matematikken I vil se herunder ændrer sig dog ikke det mindste uanset hvilken af de to geometrier man bruger.

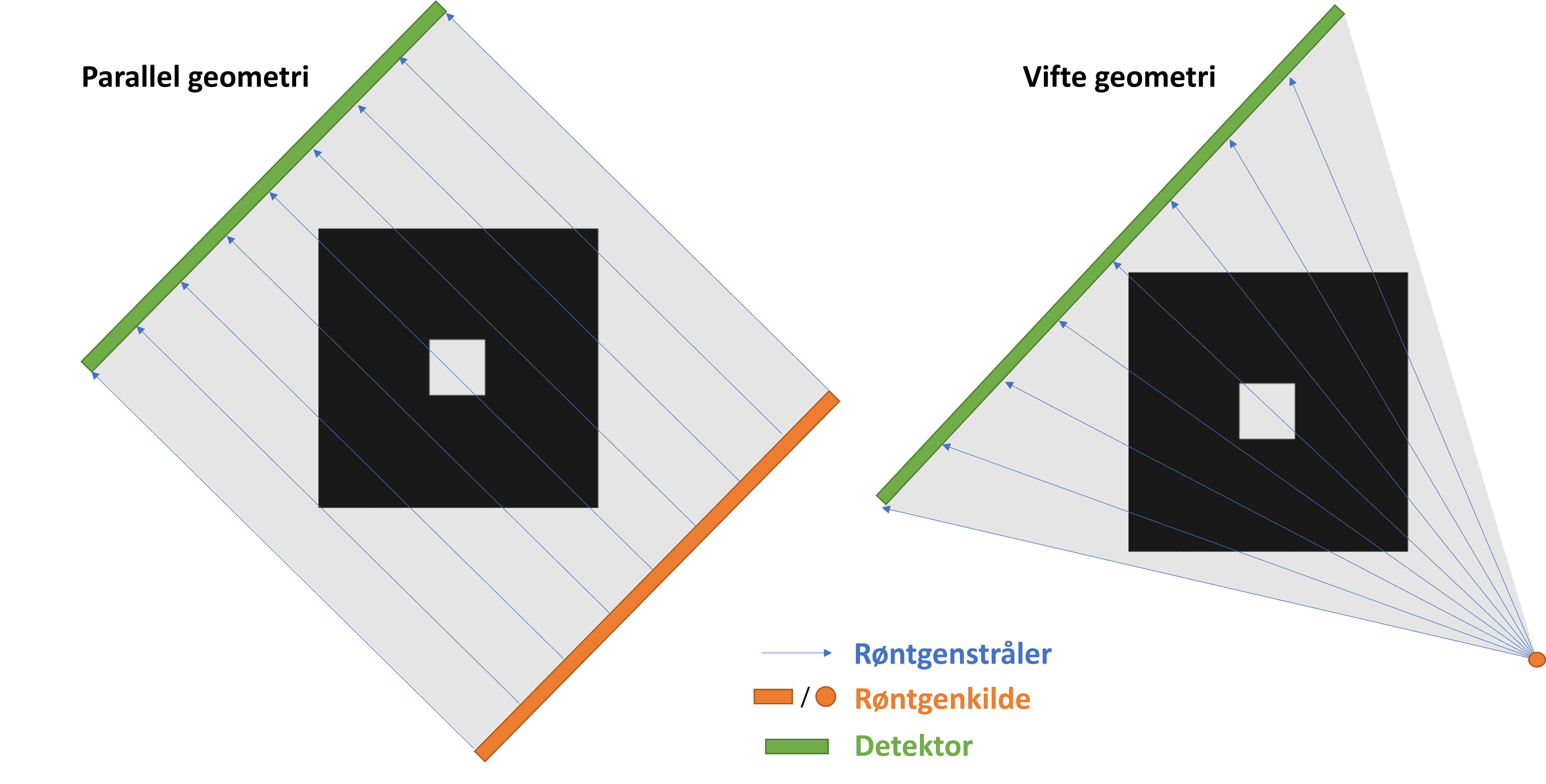
CT-skanning geometrier. Til venstre ser vi parallelle stråler og til højre ser vi vifte stråler. I begge tilfælde måler vi projektioner af et 2D objekt med et hvidt kvadrat i centrum. Det er det vi skal forsæge at rekonstruere på baggrund af målingerne.

Sinogrammer

Ofte samler vi vores målinger af røntgenabsorption i såkaldte sinogrammer. Et sinogram repræsenterer alle 1D projektioner i et plan rundt om et objekt, og det kan bruges til at rekonstruere et 2D tværsnit i det plan. Et sinogram er et billede, hvor hver pixel række indeholder 1D projektionerne fra hver vinkel. Dette er illustreret i figur 9 og 10. Billedet kaldes et sinogram fordi simple objekter vil resultere i sinusformede kurver i sinogrammet. Kurvens amplitude vil afhænge af hvor langt objektet er fra centrum af billedet, og kurvens fase vil afhænge af i hvilken retning fra centrum objektet befinder sig. Derudover er kurvens tykkelse bestemt af objektets størrelse, og kontrasten mellem kurvens værdi og baggrunden er bestemt af objektets absorptionskoefficient. I figur 11 giver vi eksempler der illustrerer disse principper.

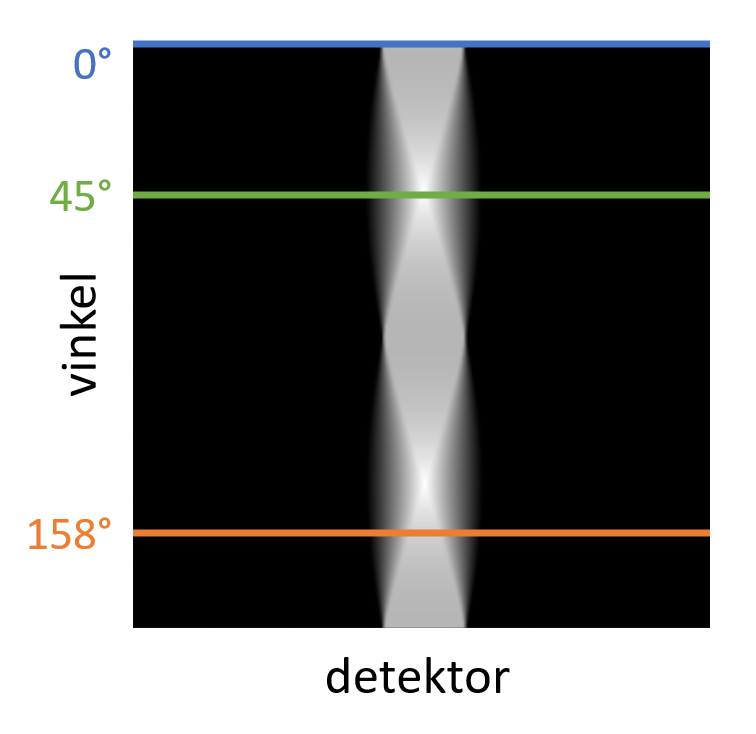
Illustration af hvordan 1D projektioner fra mange vinkler stakkes til at blive et sinogram.
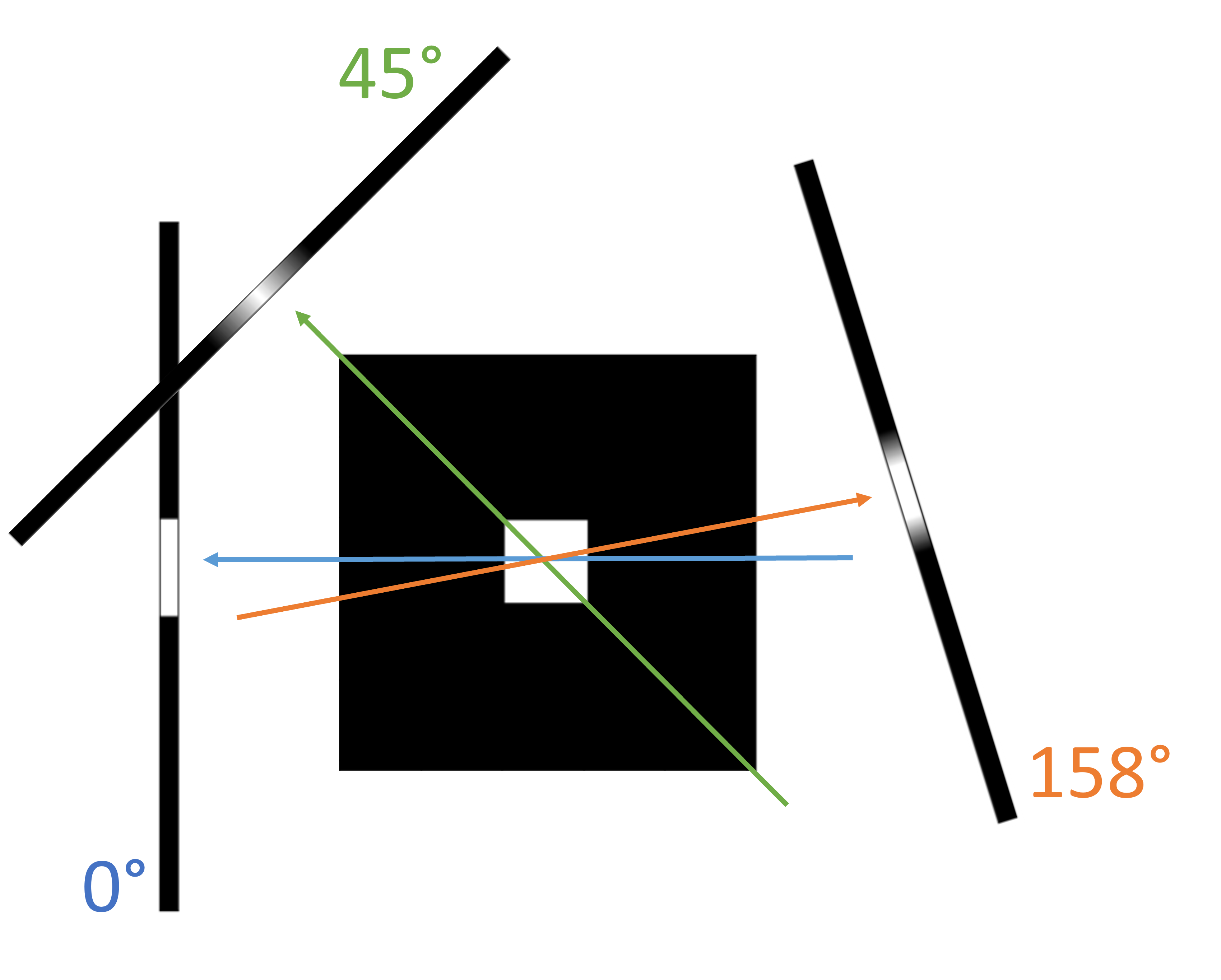
Illustration af hvordan 1D projektioner fremkommer fra et såkaldt fantom (her billede af et kvadrat) med parallel strålingsgeometri.
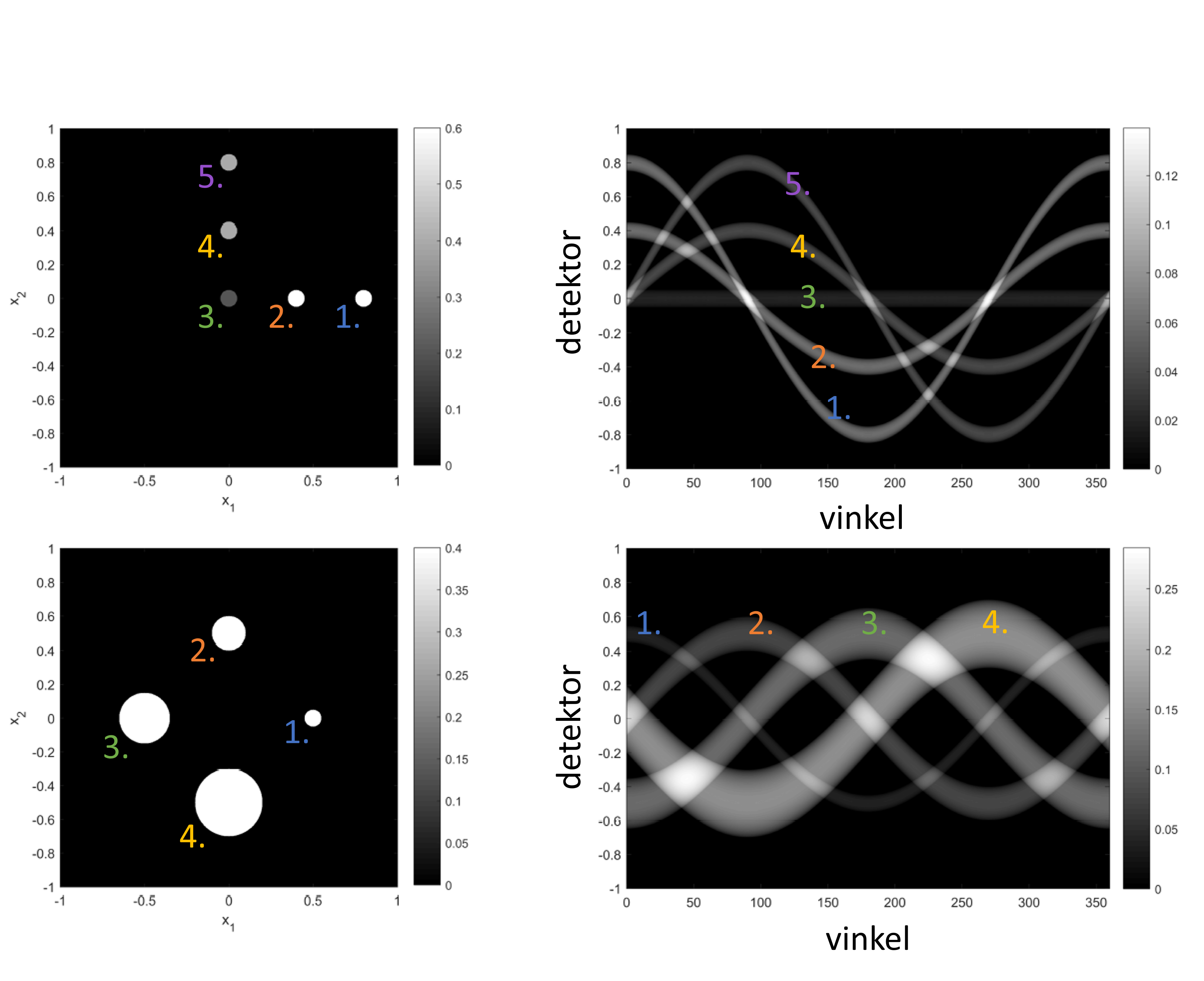
I denne figure illustrerer vi hvordan en skrives position, størrelse og kontrast til baggrunden påvirker sinogrammet. Skivens afstant til centrum påvirker kurvens amplitude. Skivens retning fra centrum påvirker kurvens fase. Skivens størrelse påvirker kurvens bredde. Skivens kontrast til baggrunden påvirker kurvens intensitet. Bemærk, vinkel og detektor akserne er byttet rundt her i forhold til figur 9. Denne figur er modificeret fra [7].

Model

I CT bruger vi modellen for absorption af stråling i materiale. I fysik har I måske allerede lært at absorption i et homogent materiale følger en eksponentiel funktion: \begin{equation} I_1 = I_0 \exp\left(-\ell_1 x_1\right), \end{equation} hvor $I_0$ er intensiteten af røntgenstrålen før den rammer noget materiale, $I_1$ er intensiteten af røntgenstrålen efter absorption i materialet, $\ell_1$ er tykkelsen af materialet, og $x_1$ er materialets absorptionskoeffcient.

Vi kunne også forestille os, at der var to materialer efter hinanden, som røntgenstrålen skulle igennem. I så fald kunne vi udtrykke røntgen intensiteteten efter begge materialer: \begin{align} I_2 &= I_1 \exp\left(-\ell_1 x_1\right) \nonumber \\ &= I_0 \exp\left(-\ell_1 x_1\right)\exp\left(-\ell_2 x_2\right). \end{align}

Hvis vi forsætter denne tanke og sætter flere materialer efter hinanden, får vi udtrykket for intensiteten efter røntgenstrålen har været igennem $k$ materialer: \begin{align} I_k &= I_0 \exp\left(-\ell_1 x_1\right) \dots \exp\left(-\ell_k x_k\right)\nonumber\\ &= I_0 \exp\left(-\ell_1 x_1 - \dots -\ell_k x_k\right) \nonumber\\ &= I_0 \exp\left( \sum_{i=1}^k -\ell_i x_i\right). \end{align} I figur 12 er røntgenabsorption i materiale illustreret.

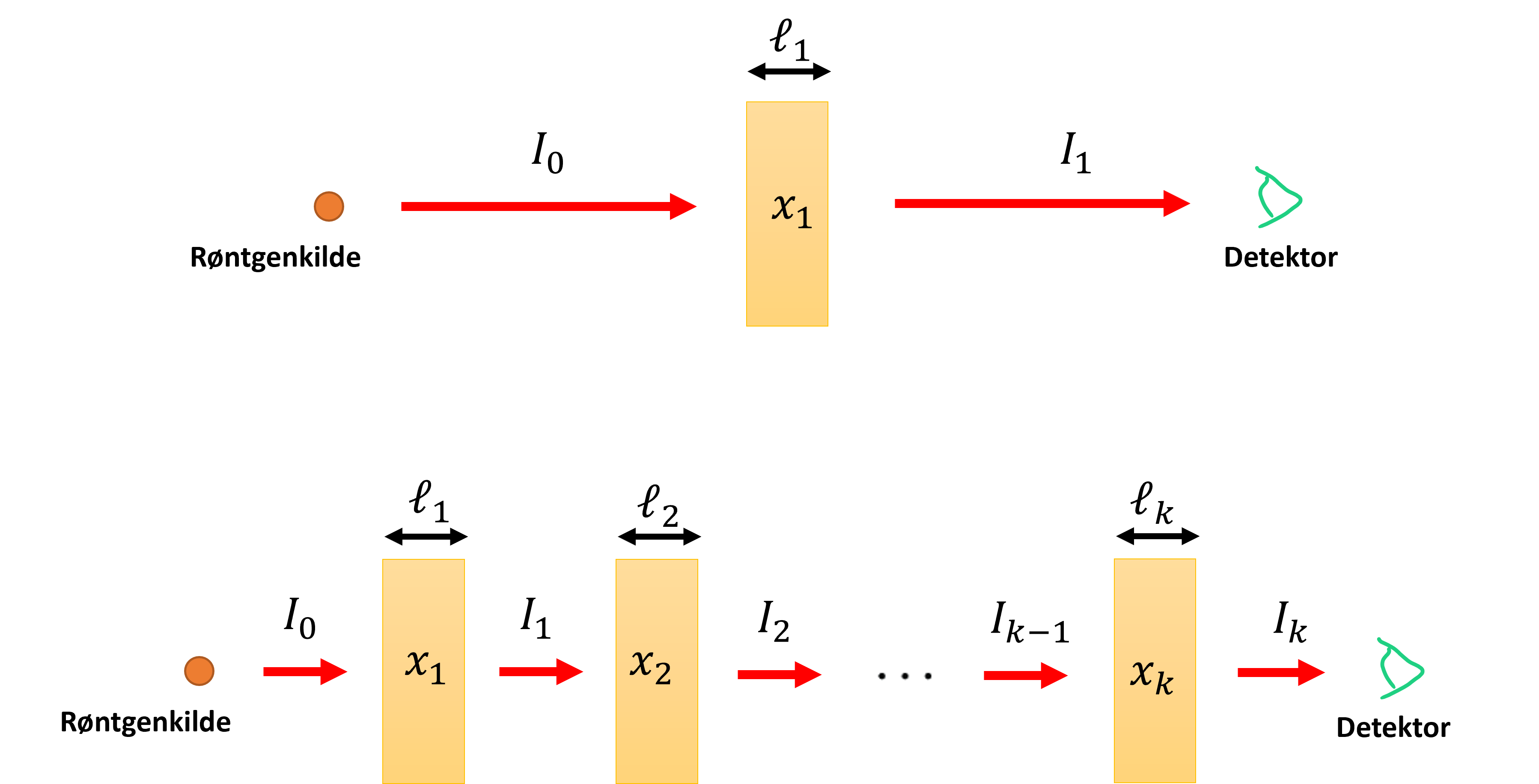
Røntgenaborption i materiale. Øverst afbilledes røntgen absorption i et enkelt homogent materiale. Nederst illusreres det hvordan røntgenintensiteten påvirkes igennem flere materialer efter hinanden.

Vi kan også koble ovenstående ligning til vores pixel billede, som vi gerne vil rekonstruere. I stedet for $k$ materialer med hver sin tykkelse, bevæger røntgenstrålen sig igennem $k$ pixels, hvor vi antager at hvert pixel har én absorptionskoefficient. I figur 13 er der illustreret et billede med $3\times 3$ pixels og 3 røntgenstråler. Vi kan skrive ligningen for hver røntgenstråles udgangsintensitet: \begin{equation} \begin{aligned} \label{eq:xray_eq} I_1 &= I_0 \exp\left( -1x_1 - 0x_2 - 0x_3 - 1x_4 - 0x_5 - 0x_6 - 1x_7 - 0x_8 - 0x_9\right)\\ I_2 &= I_0 \exp\left( -0.42x_1 - 0x_2 - 0x_3 - 0.83x_4 - 0.83x_5 - 0x_6 - 0x_7 - 0.42x_8 - 1.25x_9\right)\\ I_3 &= I_0 \exp\left( -0x_1 - \sqrt{2}x_2 - 0x_3 - 0x_4 - 0x_5 - \sqrt{2}x_6 - 0x_7 - 0x_8 - 0x_9\right) \end{aligned} \end{equation}

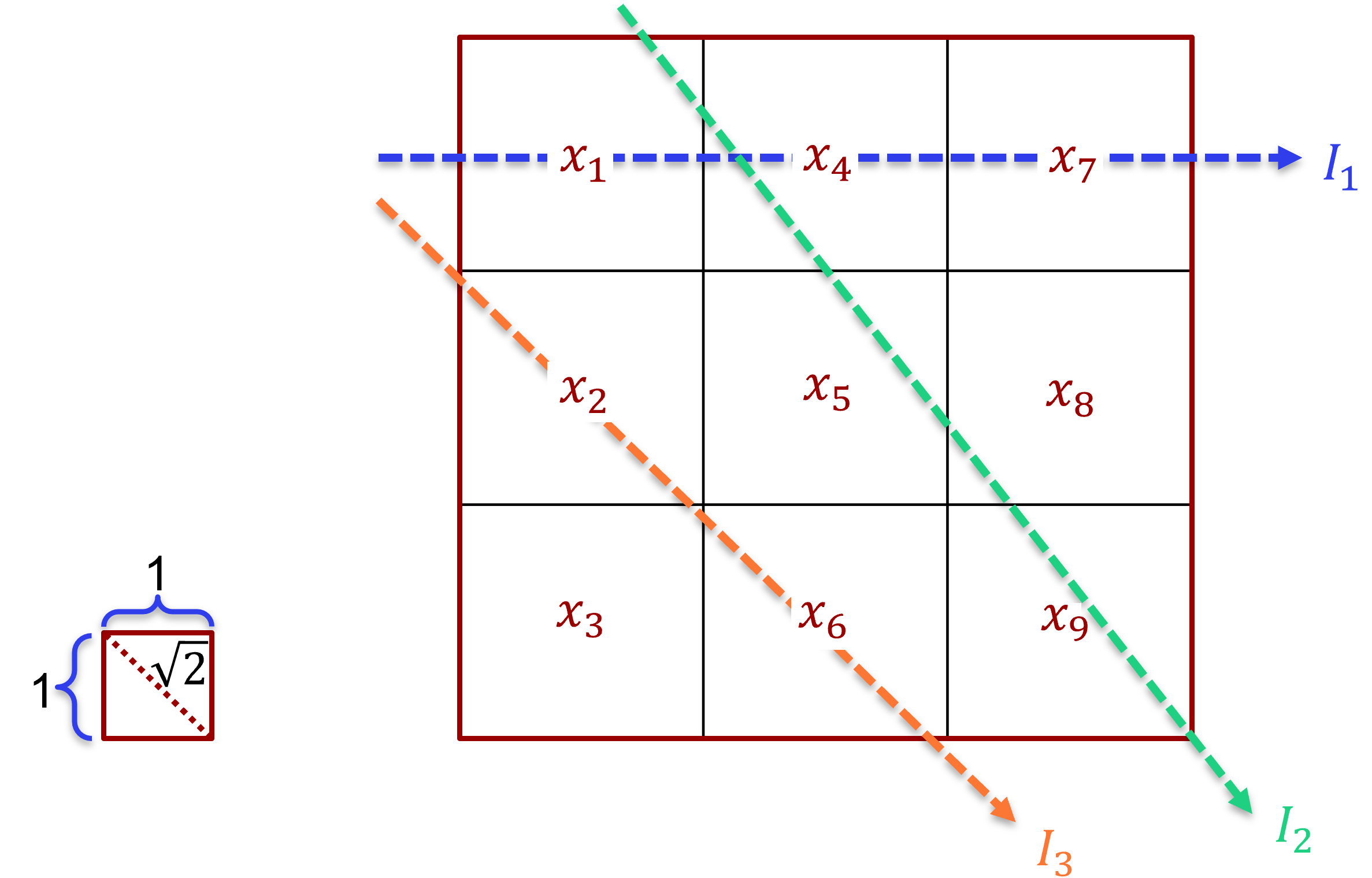
3 røntgenstråler der går igennem et $3\times 3$ pixel billede. Udtrykkene for hver stråles udgangsintensitet kan findes i (4).

Når vi skal lave CT rekonstruktion er det smart at omkrive modellen til følgende form: \begin{align} \label{eq:model} -\ln\left( \frac{I_k}{I_0}\right) = \sum_{j=1}^k \ell_j x_j. \end{align} På denne form vil man betegne $-\ln\left( \frac{I_k}{I_0}\right)$ som data, og modellen bliver lineær i parametrene $x_1, x_2, \dots, x_n$.

Nu har vi angivet modellen for hvordan en enkelt røntgenstråle bliver dæmpet i materiale. Men i CT, har vi MANGE røntgenstråler; én for hvert pixel i vores detektor gange antallet af projektioner. Vi skal altså skrive denne ligning op for samtlige røntgenstråler. Dermed får vi et stor lineært ligningssystem, og det skal vi løse for at bestemme absorptionskoefficienterne. I de næste afsnit vil du lære mere om lineære ligningssystemer, hvordan de løses, samt hvordan de skrives op for CT problemet.

Linære ligningssystemer

I dette afsnit vil vi komme nærmere ind på hvordan vi definerer, og opskriver lineære ligningssystemer. Afsnittet er baseret på [2].

En lineær ligning

En lineær ligning med $n$ ubekendte parametre $x_1, x_2, \dots, x_n$ er en ligning af formen \begin{equation} \label{eq:ligning} a_1 x_1 + a_2 x_2 + \dots + a_n x_n = b. \end{equation} Tallene $a_1, a_2, \dots, a_n$ kaldes koefficienter, og tallet $b$ kaldes højresiden. Koefficienterne og højresiden betragtes som kendte tal i modsætning til de ubekendte. Hvis $b=0$ kalder vi ligningen for homogen, og hvis $b\neq 0$ kalder vi ligningen for inhomogen.

En ligning på formen ovenfor har uendeligt mange løsninger, hvis $n>1$ og ligningen ikke er inkonsistent. En ligning er inkonsistent, hvis ikke der findes en samling parametre $(x_1, x_2, \dots, x_n)$ sådan at \eqref{eq:ligning} er opfyldt. Det kunne fx være hvis alle koefficienterne er 0 og højresiden er forskellig fra 0.

To ligninger med to ubekendte

I har måske allerede stødt på problemet vi kalder "to ligninger med to ubekendte". Det er det mindste ligningssystem vi kan forestille os og det kan generelt opskrives: \begin{equation} \begin{aligned} a_{1,1} x_1 + a_{1,2} x_2 &= b_1\\ a_{2,1} x_1 + a_{2,2} x_2 &= b_2 \end{aligned} \end{equation} Et ligningssystem som dette kan have enten ingen, én eller uendeligt mange løsninger. I figur 14 kan du se den geometriske fortolkning af disse muligheder, hvor hver ligning repræsenterer en linje i planen. Et ligningssystem med 2 ligninger med 2 ubekendte kan plottes som to linjer. Løsningen på ligningssystemet kan findes ved at bestemme skæringen mellem linjerne. Hvis systemet har én løsning, er der ét skæringspunkt, hvis systemet ingen løsninger har, er linjerne parallelle, og hvis der er uendeligt mange løsninger, ligger linjerne oveni hinanden. Uendeligt mange løsninger opstår når ligningerne er lineært afhængige af hinanden. Vi vender tilbage til, hvad det betyder.

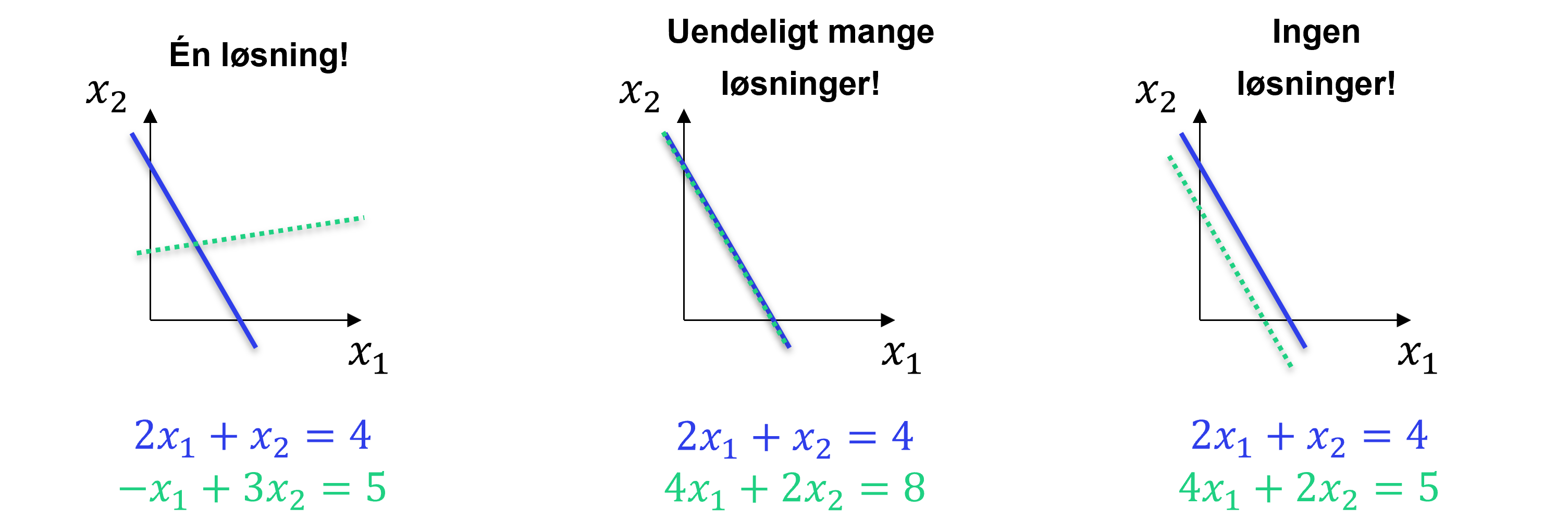
Illustration hvilke mulige løsningstyper vi har i et system med to ligninger og to ubekendte.

Ligningssystemer

Et linæert ligningssystem består af $m$ ligninger af typen \eqref{eq:ligning} med $n$ ubekendte. Det kan opskrives: \begin{equation} \begin{aligned} a_{1,1} x_1 + a_{1,2} x_2 &+ + a_{1,n} x_n = b_1 \\ a_{2,1} x_1 + a_{2,2} x_2 &+ + a_{2,n} x_n = b_2\\ &\vdots\\ a_{m,1} x_1 + a_{m,2} x_2 &+ + a_{m,n} x_n = b_m \label{eq:ligningssystem} \end{aligned} \end{equation}

Ligesom for en enkelt lineær ligning kalder vi tallene $a_{1,1}, \dots, a_{m,n}$ for koefficienter, og tallene $b_1,\dots,b_m$ kaldes højresiden. Hvis alle tallene på højresiden er lig nul, $b_1=b_2=\dots=b_m=0$, kaldes systemet for homogent, men hvis blot et enkelt af de tal er forskellige fra nul kaldes systemet for inhomogent.

Ligesom for "to ligninger med to ubekendte" kan vi have ingen, én eller uendeligt mange løsninger. Ligningssystemet har netop én løsning, hvis der er $m$ lineært uafhængige ligninger med $n$ ubekendte. I det tilfælde siger vi at systemet er entydigt bestemt. Hvis der er flere ubekendte end lineært uafhængige ligninger, vil der være uendeligt mange løsninger. Det kaldes et underbestemt problem, fordi der ikke er nok information i ligningerne til at løse systemet. Den sidste mulighed er, at der ikke findes nogen løsninger til systemet. Det kan forekomme, hvis der er flere lineært uafhængige ligninger, end der er ubekendte, og at disse ligninger er inkonsistente med hinanden. Sådan et problem kaldes overbestemt fordi ligningerne giver for meget og modstridende information.

Vi kan bruge lineære ligningssystemer til at beskrive de talpuslespil vi startede med. Desuden har vi nu fået sat ord på at talpuslespil a) er underbestemt, b) er entydigt bestemt, og c) er overbestemt. Herunder giver vi ligningssystemerne for talpuslespil a)-c).
a) \begin{equation} \begin{aligned} x_1 + x_3 &= 5\\ x_2 + x_4 &= 2\\ x_1 + x_2 &= 3\\ x_3 + x_4 &= 4 \end{aligned} \end{equation}
b) \begin{equation} \begin{aligned} x_1 + x_3 &= 5\\ x_2 + x_4 &= 2\\ x_1 + x_2 &= 3\\ x_3 + x_4 &= 4\\ \sqrt{2}x_1 + \sqrt{2}x_4 &= \sqrt{2} \end{aligned} \end{equation}
c) \begin{equation} \begin{aligned} x_1 + x_3 &= 5.1\\ x_2 + x_4 &= 1.8\\ x_1 + x_2 &= 2.9\\ x_3 + x_4 &= 4.2\\ \sqrt{2}x_1 + \sqrt{2}x_4 &= 1.3 \end{aligned} \end{equation}

Struktursætningen

Hvis vores lineære ligningssystem er underbestemt, er der ikke information nok til at løse systemet entydigt. Der er uendeligt mange løsninger. Den uendelige løsningsmængde kan udtrykkes ved det vi kalder \textit{struktursætningen}: \begin{equation} \mathcal{L}_{inhom} = x_{inhom} + k\cdot x_{hom}, \end{equation} hvor $\mathcal{L}_{inhom}$ er løsningsmængden til det inhomogene system, $x_{inhom} = (x_{1,inhom}, x_{2,inhom}, \dots, x_{n,inhom})$ er én vilkårlig løsning til det inhomogene system, $x_{hom} = (x_{1,hom}, x_{2,hom}, \dots, x_{n,hom})$ er én vilkårlig løsning til det homogene system og $k$ er et hvilket som helst tal. Ved at vælge forkellige $k$ kan vi finde forskellige løsninger til systemet. Fordi antallet af mulige $k$ er uendelig, er det også uendeligt mange løsninger til systemet.

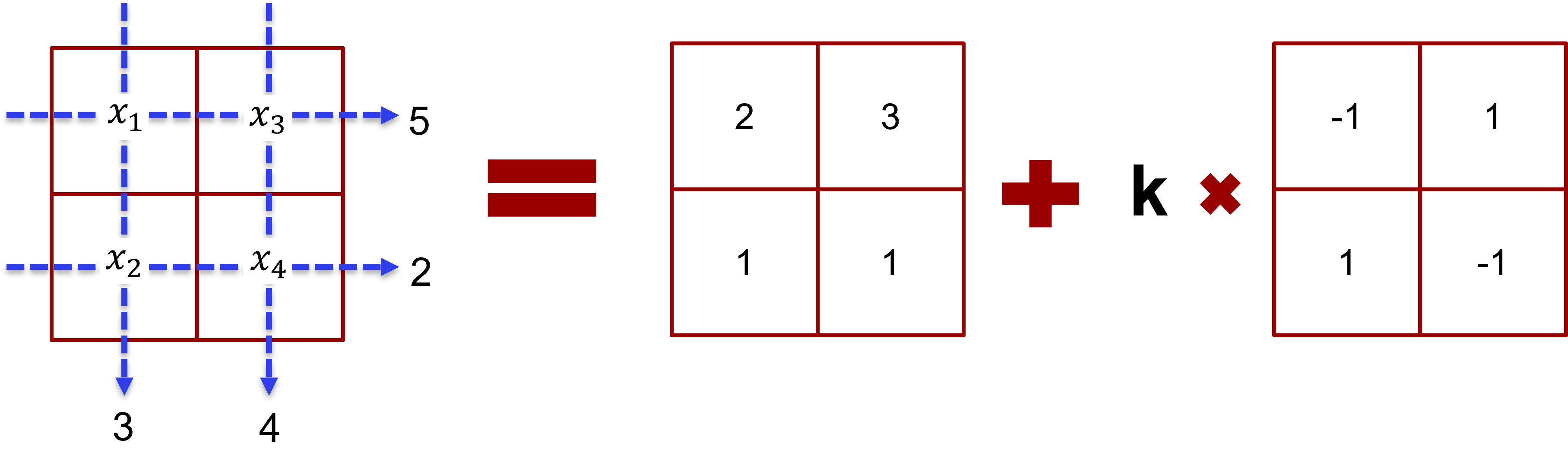
Løsningsmængden til talpuslespil a) angivet vha. struktursætningen.
I figur 15 bruger vi struktursætningen til at vise løsningsmængden til talpuslespil a). Vi kan skrive løsningen: \begin{equation} \begin{aligned} x_1 &= 2-k\\ x_2 &= 1+k\\ x_3 &= 3+k\\ x_4 &= 1-k. \end{aligned} \end{equation} Vi kan altså få forskellige løsninger ved at vælge forskellige $k$. Fx, får vi for $k=1$: \begin{equation} \begin{aligned} x_1 &= 1\\ x_2 &= 2\\ x_3 &= 4\\ x_4 &= 0, \end{aligned} \end{equation} og for $k=5$ får vi: \begin{equation} \begin{aligned} x_1 &= -3\\ x_2 &= 6\\ x_3 &= 8\\ x_4 &= -4. \end{aligned} \end{equation} Prøv selv at tjekke at disse løsninger passer og find evt. nogle flere.

Lineært (u)afhængige ligninger

En afhængig ligning i et ligningssystem kan skrives som en linearkombination af de resterende ligninger i systemet. I et system af lineært uafhængige ligninger kan ingen af ligningerne skrives som en linearkombination af de resterende ligninger. Vi er altså nødt til at vide, hvad en linearkombination betyder. Med en ikke helt stringent matematisk notation kan vi skrive linearkombinationen af ligninger som: \begin{equation} L_m: c_1 L_1 + c_2 L_2 + \dots + c_{m-1} L_{m-1}, \end{equation} hvor $L_i$ representerer en ligning i systemet, $c_i$ er en konstant og $i=1,\dots,m$. Med denne notation menes det at fx $c_1$ ganges på både højre- og venstresiden af ligning $L_1$, og summen $c_1 L_1 + c_2 L_2$ betyder at venstresiderne lægges sammen og højresiderne lægges sammen. Herunder giver vi nogle eksempler på lineært afhængige ligninger.

\begin{equation} \begin{aligned} L_1:& \quad x_1 + 2x_2 = 2\\ L_2:& \quad 2x_1 + 4x_2 = 4 \end{aligned} \end{equation} I dette ovenstående ligningssystem er ligningerne lineært afhængige af hinanden fordi den anden ligning kan skrives ved at gange den første ligning med 2. Altså $L_2: 2 L_1$
\begin{equation} \begin{aligned} L_1:& \quad x_1 + 2x_2 + 3x_3 = 3\\ L_2:& \quad 3x_1 + x_2 + 5x_3 = 6\\ L_3:& \quad 4x_1 + 3x_2 + 8x_3 = 9 \end{aligned} \end{equation} I dette ovenstående ligningssystem er ligningerne lineært afhængige af hinanden fordi den sidste ligning kan skrives ved at lægge de andre to sammen. Altså $L_3: L_1 + L_2$.
\begin{equation} \begin{aligned} L_1:& \quad x_1 + 2x_2 + 3x_3 = 3\\ L_2:& \quad 3x_1 + 4x_2 + 5x_3 = 6\\ L_3:& \quad 7x_1 + 8x_2 + 9x_3 = 12 \end{aligned} \end{equation} I dette ovenstående ligningssystem er ligningerne lineært afhængige af hinanden fordi den sidste ligning kan skrives ved at gange ligning 2 med 3 og trække den første ligning fra 2 gange. Altså $L_3: 3L_2 - 2L_1$.
\begin{equation} \begin{aligned} L_1:& \quad x_1 + 2x_2 = 4\\ L_2:& \quad 2x_1 - 2x_2 = 2\\ L_3:& \quad 4x_1 - 4x_2 = 4 \end{aligned} \end{equation} I dette ovenstående ligningssystem er ligningerne lineært afhængige af hinanden fordi den sidste ligning kan skrives $L_3: 2L_2$. Hvis vi fjerner $L3$ (eller $L_2$) står vi tilbage med et system af lineært uafhængige ligninger.
Vi kan nu forklare, hvorfor talpuslespil a) er underbestemt. Ligningssystemet var givet: \begin{equation} \begin{aligned} L_1:& \quad x_1 + x_3 = 5\\ L_2:& \quad x_2 + x_4 = 2\\ L_3:& \quad x_1 + x_2 = 3\\ L_4:& \quad x_3 + x_4 = 4 \end{aligned} \end{equation} Det indeholder lineært afhængige ligninger fordi $L_1: L_3 + L_4 - L_2$. Vi har altså kun 3 lineært uafhængige ligninger men 4 ubekendte.

CT ligningssystemet

Lad os vende tilbage til CT problemet. Vi har tidligere defineret modellen for hvordan én røntgenstråle dæmpes i materiale. Men i CT problemet udsender vi jo mange stråler fra mange vinkler, så for at få al informationen med i CT problemet definerer vi det som et lineært ligningssystem: \begin{equation} \begin{aligned} \sum_{j=1}^n \ell_{1,j} x_j &= -\ln\left( \frac{I_1}{I_0}\right)\\ \sum_{j=1}^n \ell_{2,j} x_j &= -\ln\left( \frac{I_2}{I_0}\right)\\ \vdots\\ \sum_{j=1}^n \ell_{m,j} x_j &= -\ln\left( \frac{I_m}{I_0}\right) \end{aligned} \end{equation} Hvis vi sammenligner med definationen af et lineært ligningssystem, kan vi se, at for CT problemet er koefficienterne i systemet $a_{i,j} = \ell_{i,j}$, som beskriver længden på røntgenstråle $i$'s vej gennem pixel/voxel $j$. Bemærk, at langt de fleste koefficienter vil være 0 fordi en enkelt røntgenstråle kun krydser en brøkdel af pixels/voxels. Højresiderne er givet som $b_i = -\ln\left( \frac{I_i}{I_0}\right)$ og indeholder den målte udgangsintensitet for røntgenstråle $i$. I figur 16 viser vi en røntgenstråles vej gennem rekonstruktionsdomænet.

I CT vil vi i praksis aldrig have en entydig løsning. Ofte skal der rekonstrueres flere parametre/pixels end vi har målepunkter hvilket gør problemet underbestemt. Der kan også nemt opstå inkonsistens i ligningssystemet, fordi vi aldrig kan lave helt nøjagtige målinger, der vil altid være måleusikkerhed. Derfor har vi brug for en robust metode til at løse ligningssystemer, der både kan være underbestemte, overbestemte og inkonsistente.

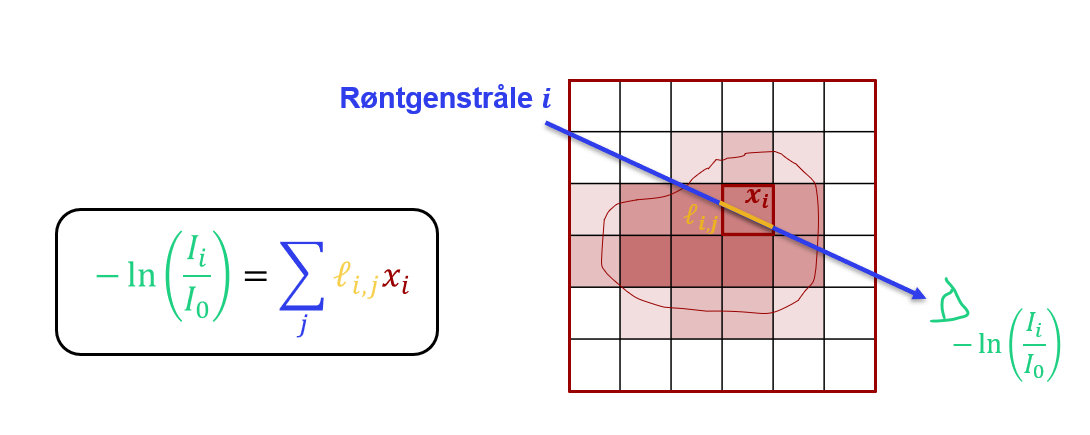
Illustration af hvordan vi opstiller ligningerne i CT forward problemet.

Rekonstruktion

I de tidligere afsnit har vi studeret CT problemet og hvordan CT data opstår. Nu er det tid til at kigge på, hvordan vi laver en CT rekonstruktion. Der findes mange forskellige metoder til CT rekonstruktion, men vi vil fokusere på mindste kvadraters metode. Det er en meget udbredt metode, der bruges til at løse lineære ligningssystemer i alle mulige sammenhænge. I har måske allerede stødt på mindste kvadraters metode når I laver regression. I lineær regression, f.eks., bestemmer man en linjes ligning ud fra en samling af punkter ved at minimere kvadratet af hvert punkts afstand til linjen. Herunder beskrives mindste kvadraters metode for et generelt lineært ligningssystem.

Mindste kvadraters metode

Overbestemte problemer

Når vi skal løse et overbestemt lineært ligningssystem med mindste kvadraters metode, minimerer vi summen af kvadraterne af residualerne. Residualerne er kort sagt højresiden minus venstresiden i hver ligning. Vi kan skrive mindste kvadraters metode som: \begin{align} &\text{Bestem $(x_1, x_2, \dots, x_n)$ sådan at de minimerer:} \nonumber \\ &\sum_{i = 1}^m \left( a_{i,1} x_1 + a_{i,2} x_2 + \dots + a_{i,n} x_n - b_i\right)^2. \label{eq:lsq} \end{align} Det ser måske noget kompliceret ud, og det kan det også sagtens blive. Men for meget små systemer kan vi godt løse problemet i hånden. Lad os se på et eksempel:

Geometrisk illustration af 3 ligninger med 2 ubekendte samt mindste kvadraters metode løsningen af systemet.

Vi vil løse det følgende ligningssystem for $x_1$ og $x_2$: \begin{equation} \begin{aligned} 2x_1 - x_2 &= 1\\ -x_1 + 4x_2 &= 8\\ 3x_1 + x_2 &= 4. \label{eq:lsq_ex_system} \end{aligned} \end{equation} Hvis vi plotter ligningernes linjer, ser vi hurtigt at systemet ikke har en løsning (figur 17). De skærer nemlig ikke alle sammen hinanden i samme punkt. Systemet er altså overbestemt og vi vil bruge mindste kvadraters metode til at finde den bedste løsning. Først indsætter vi systemet i formel \eqref{eq:lsq}: \begin{align} &\text{Bestem $x_1$ og $x_2$ sådan at de minimerer:} \nonumber \\ &\left(2x_1 - x_2 - 1\right)^2 + \left(-x_1 + 4x_2 - 8\right)^2 + \left(3x_1 + x_2 - 4\right)^2. \label{eq:min_ex} \end{align} Og hvordan løser vi så dette minimeringsproblem? Jo, I har sikkert allerede stødt på optimeringsproblemer i gymnasiet, hvor man differentierer og sætter lig nul. Det er sådan set fuldstændig det samme her. Den eneste forskel er, at vi skal lave partiel differentiation. Altså differentiere mht. hver af de ubekendte vi løser for. Først differentierer vi udtrykket i \eqref{eq:min_ex} mht. $x_1$ (så ses $x_2$ som en konstant): \begin{align} 0 &= \frac{\partial}{\partial x_1} \left( \left(2x_1 - x_2 - 1\right)^2 + \left(-x_1 + 4x_2 - 8\right)^2 + \left(3x_1 + x_2 - 4\right)^2\right)\nonumber\\ &= 4(2x_1 - x_2 - 1) - 2(-x_1 + 4x_2 - 8) + 6(3x_1+x_2-4)\nonumber\\ &= 28x_1 -6x_2 -12. \label{eq:lsq_L1} \end{align} Så differentierer vi mht. $x_2$ (hvor $x_1$ ses som en konstant): \begin{align} 0 &= \frac{\partial}{\partial x_2} \left( \left(2x_1 - x_2 - 1\right)^2 + \left(-x_1 + 4x_2 - 8\right)^2 + \left(3x_1 + x_2 - 4\right)^2\right)\nonumber\\ &= -2(2x_1 - x_2 - 1) +8(-x_1 + 4x_2 - 8) + 2(3x_1+x_2-4)\nonumber\\ &= -6x_1 + 36 x_2 -70. \label{eq:lsq_L2} \end{align} Hvis vi kombinerer \eqref{eq:lsq_L1} og \eqref{eq:lsq_L2} har vi et lineært ligningssystem med 2 ligninger og 2 ubekendte. Løsningen til dette system vil give os de $x_1$ og $x_2$ der minimerer \eqref{eq:min_ex}: \begin{equation} \begin{aligned} 0 &= -28x_1 -6x_2 -12\\ 0 &= -4x_1 + 36 x_2 -74 \end{aligned} \Leftrightarrow \begin{aligned} x_1 &\approx 0.88 \\ x_2 &\approx 2.09. \end{aligned} \end{equation} Dette er altså mindste kvadraters løsningen til ligningssystemet i (24) og det er vist i en geometrisk fortolkning i figur 17.

Talpuslespil c) løst med mindste kvadraters metode.

Lad os også vende tilbage til vores talpuslespil. I figur 18 viser vi igen talpuslespil c). Vi har et overbestemt system, hvor ligningerne er inkonsistente. Vi overlader det som en øvelse at beregne mindste kvadraters løsningen, men angiver resultatet i figuren. Fremgangsmåden er tilsvarende eksemplet ovenfor, denne gang har vi bare 4 ubekendte, så vi skal differentiere mht. hver af dem. Det vil lede til et ligningssystem med 4 ligninger og 4 ubekendte, der skal løses for at finde mindste kvadraters løsningen til talpuslespillet. Hvis vi indsætter den fundne løsning i talpuslespillet ser vi hurtigt, at den ikke stemmer overens med målingerne, hvilket forventes, fordi systemet er inkonsistent.

Eksemplerne ovenfor viser os, at selv for det et meget simpelt ligningssystem, kan det hurtigt blive lange beregninger, hvis man skal lave dem i hånden. Derfor bruger man faktisk altid en computer til at beregne en mindste kvadraters løsning. Computeren har smarte måder at implmentere løsningen på, men det kræver, at man kan opskrive ligningssystemt på matrix form. På øvelsesdagen lader vi et program opskrive ligningssystemet på matrix form for os, når vi skal løse CT problemet på en computer. Se evt. foreslag til yderligere fordybelse for at komme igang med at skrive lineære ligningssystemer på matrix form.

Entydigt bestemte problemer

Hvis vores ligningssystem har en entydig løsning, behøver vi ikke mindste kvadraters metode til at løse det. Vi kan fx bruge substitution eller andre metoder kendt fra to ligninger med to ubekendte. Men, hvis man bruger mindste kvadraters metode, vil man også få den korrekte entydige løsning. Det er bare lidt en omvej.

Talpuslespil b) med sin entydige løsning.

I talpuslespil b) havde vi en entydig løsning. Den kan som nævnt finde vha. mindste kvardraters metode, det er bare en omvej. Som en øvelse, kan man forsøge at løse ligningssystemet med de metoder I allerede kender fra 2 ligninger med 2 ubekendte. Hvis man kender til matricer eller vælger at inddrage matrixregning i sin SRP, er det en fordel at skrive ligningssystemet op på matrixform. Så kan man løse systemet med GaussJordan-elimination, som man kan læse mere om i [2]. Udvidelsen til matrixform at ligningssystemer er en god mulighed for yderligere fordybelse i en SRP om CT.

Underbestemte problemer

Bemærkning: Dette afsnit kommer ind på nogle avancerede problematikker og metoder. Resten af materialet kan sagtens stå alene, så brug kun dette afsnit, hvis du gerne vil udfordres.

Vi har allerede fastslået at underbestemte problemer har uendeligt mange løsninger. Hvis vi gerne vil have én god løsning til det underbestemte problem er vi nødt til at opstille endnu et kriterium, der gør, at vi kan få en entydig løsning. Ofte er dette kriterium, at vi leder efter den "mindste" løsning der løser ligningssystemet. I en forstand repræsenterer det den simpleste løsning, og i den fysiske verden er den simpleste løsning ofte den bedste ifølge Ockhams princippet [3].

Der findes mange metoder til at vælge én løsning til et underbestemt problem. Her giver vi et eksempel på en af de mere simple metoder, som bl.a. bliver anvendt i det meget udbredte Python bibliotek "numpy". Vi vælger den løsning fra løsningsmængden der er "mindst" i mindste kvadraters forstand, altså: \begin{align} &\text{Vælg $k$ så den minimerer:} \nonumber \\ &(x_{1,inhom} + k \cdot x_{1,hom})^2 + (x_{2,inhom} + k\cdot x_{2,hom})^2 + \dots +(x_{n,inhom} + k \cdot x_{n,hom})^2. \label{eq:lsq_underbestemt} \end{align} Lad os forsøge at implementere dette i vores talpuslespil der er underbestemt.

Den "mindste" løsning til talpuslespil a).

Fra struktursætningen ved vi at løsningsmængden til talpuslespil a) er: \begin{equation} \begin{aligned} x_1 &= 2-k\\ x_2 &= 1+k\\ x_3 &= 3+k\\ x_4 &= 1-k. \end{aligned} \end{equation} Hvis vi vil have en entydig løsning, kan vi finde den "mindste" løsning ifølge \eqref{eq:lsq_underbestemt}: \begin{align} &\text{Vælg $k$ så den minimerer:} \nonumber \\ &(2 - k)^2 + (1 + k)^2 + (3 + k)^2 + (1 - k)^2. \end{align} For at minimere udtrykket differentierer vi mht. $k$ og sætter lig nul: \begin{align} 0 &= \frac{d}{dk} (2 + k\cdot (-1))^2 + (1 + k\cdot 1)^2 + (3 + k\cdot 1)^2 + (1 + k\cdot (-1))^2\nonumber \\ &= -2(2-k) + 2(1+k) + 2(3+k) - 2(1-k). \end{align} Vi løser ovenstående for $k$, så vi får $k=-\frac{1}{4}$. Indsætter vi det i løsningen fra struktursætningen for vi: \begin{equation} \begin{aligned} x_1 &= 2+\tfrac{1}{4} = 2.25\\ x_2 &= 1-\tfrac{1}{4} = 0.75\\ x_3 &= 3-\tfrac{1}{4} = 2.75\\ x_4 &= 1+\tfrac{1}{4} = 1.25 \end{aligned} \end{equation} I virkeligheden kan vi ikke vide, om dette er den løsning, der gav anledning til målingerne. Og i dette tilfælde stemmer de heller ikke overens. Grunden til at vi valgte netop denne løsning er, at den opfylder et yderligere kriterium, som repræsenterer, hvad vi tror gælder om løsningen; nemlig at løsningen skal være den mindst mulige.

CT rekonstruktion

Nu har vi set, hvordan CT problemet kan skrives som et lineært ligningssystem, og hvordan mindste kvadraters metode kan bruges til at løse det. CT problemer vil i praksis aldrig forekomme som entydigt bestemte problemer. Vi kan have et overbestemt problem, hvor måleusikkerhed skaber inkonsistens mellem ligningerne. I det tilfælde bruger vi mindste kvadraters metode for overbestemte problemer til at lave en rekonstruktion. Men ofte har vi et underbestemt problem, som har uendeligt mange løsninger. Der findes mange forskellige metoder til at vælge den bedste løsning. Vi gennemgik en metode, der valgte den "mindste løsning", og denne metode bruges fx af det meget udbredte Python bibliotek "numpy".

For et storskala ligningssystem, som vi har i CT, er vi nødt til at benytte os af en computer for at løse det. I figur 21 viser vi et eksempl på 2D CT rekonstruktion af et tværsnit af en valnød. Vi viser, hvordan rekonstruktionen ser ud med forskellige mængder data. Bemærk, at jo mindre data vi har, jo sværere bliver det at rekonstruere billedet. Og hvorfor optager man så ikke bare altid meget data? Det kan der være flere grunde til. Først og fremmest er røntgenstråling skadeligt for biologisk materiale og derfor vil man helst begrænse strålingsdosis så meget som muligt [4]. I industrielle applikationer kan det være et spørgsmål om tid/penge. Hvis man skal optage mere data tager det længere tid, og det kan have en effekt på prisen af undersøgelsen. Derfor kan der forekomme CT skanninger med begrænset antal projektioner, og det er stadigvæk et aktivt forskningsfelt at finde gode rekonstruktionmetoder når datamængden er begrænset.

Mindste kvadraters metode rekonstruktion af en CT-skanning af en valnød. Med færre projektioner bliver rekonstruktionerne dårligere.

Generalisering til 3D

I materialet ovenfor har vi arbejdet med CT rekonstruktion i 2D. Her vil vi sætte et par ord på, hvordan det generaliseres til 3D.

I 3D er vores ubekendte parametre stadigvæk absorptionskoefficienter, men de er ikke længere arrangeret i et billede, hvor hvert pixel repræsenterer én absorptionskoefficient. I stedet er de arrangeret i et volumen, hvor hver voxel repræsenterer én absorptionskoefficient. I dette tilfælde har vi $n=N\times N\times N$ voxels, hvor $N$ er antallet af voxels i en række/kolonne/lag. Det er illustreret i figur 22.

I denne figur ser vi hvordan vi hvordan et volumen kan repræsenteres af voxels, som er små kuber.

I 3D CT-skanninger er vores data 2D projektioner af objektet. Røntgenstrålingen vil bestråle hele objektet fra én side på én gang og detektoren på den anden side vil bestå af en flade med mange detektor pixels, som hver optager intensitet. Dvs. at det vi måler, faktisk er det, som vi normalt kender som et røntgenbillede, se figur 23. En samling af 2D projektioner fra mange vinkler er det data, der skal bruges til at lave en 3D rekonstruktion

Projektioner der bruges som data i CT. Her ser vi 2D projektioner af en 3D torso. Figuren er lånt fra [8].

Modellen for røntgenabsorption i materiale ændrer sig ikke, og det gør metoden med at skrive et lineært ligningssystem op, der skal løses med mindste kvadraters metode heller ikke. Den eneste forskel er, at vi ikke længere skal forestille os røntgenstråler, der krydser en 2D flade som i vores talpuslespil. I stedet går røntgenstrålerne igennem et volumen. Men det ændrer ikke på at strålernes vej gennem hvert voxel har en længde $\ell$, som bruges til at skrive ligningssystemet op. Vi skal altså stadigvæk skrive en ligning for hver enkelt røntgenstråle og løse det store ligningssystem med mindste kvadraters metode.

Foreslag til videre arbejde

I dette afsnit giver vi noge foreslag til yderligere matematisk fordybelse. Det vil ikke blive gennemgået på øvelsesdagen, men man kan bruge det som ekstra materiale i sin SRP.

Matrixformen af CT problemet

Når vi skal løse lineære ligningssystemer er det smart at bruge det vi kalder matrixformen af systemet. Faktisk vil en computer så godt som altid have systemet på matrix form. Studér [2] og [5] og beskriv hvorfor vi kan opskrive CT problemet som: \begin{align} \vec{A}\vec{x} = \vec{y} \quad \Leftrightarrow \quad \begin{bmatrix} \ell_{1,1} & \ell_{1,2} & \dots & \ell_{1,n}\\ \ell_{2,1} & \ell_{2,2} & \dots & \ell_{2,n}\\ \vdots & \vdots & \ddots & \vdots \\ \ell_{m,1} & \ell_{m,2} & \dots & \ell_{m,n} \end{bmatrix} \begin{bmatrix} x_1 \\ x_2 \\ \vdots \\ x_n \end{bmatrix} = \begin{bmatrix} -\ln\left(\frac{I_1}{I_0}\right)\\ -\ln\left(\frac{I_2}{I_0}\right)\\ \vdots\\ -\ln\left(\frac{I_m}{I_0}\right) \end{bmatrix} \end{align} Du kan også studere GaussJordan-elimination i [2] og øve dig i at anvende det til at løse vores talpuslespil.

Den kontinuerte model

Vi kan også udlede modellen i ligning \eqref{eq:model} ved at løse en differentialligning og diskretisere derefter. Røntgenaborption i sammensat materiale følger Lambert-Beers lov og er givet som en første ordens lineær differentialligning: \begin{equation} \frac{dI(\ell)}{d\ell} = -x(\ell)I(\ell), \end{equation} med grænsebetingelser \begin{equation} \begin{aligned} &I(\ell_0) = I_0\\ &x(\ell\leq \ell_0) = 0\\ &x(\ell\geq \ell_k) = 0. \end{aligned} \end{equation} Her har vi IKKE et homogent materiale, så værdierne af absorptionskoefficienterne $x$ og strålingsintensiteterne $I$ varierer som funktion af $\ell$.

Gode øvelser til SRP'en kunne være:

  1. Giv en fysisk forklaring på grænsebetingelserne under antagelse af at objektet ligger mellem $\ell_0$ og $\ell_k$.

    Hint: Hvor meget røntgenstråling absorberer luft?

  2. Løs differentialligningen for $I(\ell)$.

    Hint 1: Panserformel eller separation af de variable. Husk at udnytte grænsebetingelser.

    Hint 2: Svaret skal være $I(\ell) = I_0 \exp\left( \int_{\ell_0}^{\ell} x(\ell) d\ell \right)$.

  3. Diskretiser løsningen til differentialligningen og omskriv den til at være ens med ligning \eqref{eq:model}.

    Hint 1: Hvad er den diskrete udgave af et integrale?

    Hint 2: Udnyt at $I(\ell_k) = I_k$.

Iterative minimeringsmetoder

Når man skal løse minimeringsproblemer, som vi fx så i mindste kvadraters metode, er det ikke altid praktisk at finde en analytisk løsning som vi gjorde. I stedet kan man anvende iterative minimeringsmetoder, som går ud på, at man starter i et punkt og tager små skridt i retning af minimumspunktet. En af de første basale iterative minimeringsmetoder der er værd at studerere er Gradient descent metoden. I denne metode angiver en såkaldt gradient retningen vi tager skridt i. Gradienten er egentlig bare en vektor, der indeholder differentialkvotienten mht. hver variabel. Dvs. hver gang vi tager et skridt, vælger vi at gå nedad den stejleste retning fra der, hvor vi står. Hvis vi ønsker at minimere funktionen $f(x_1, x_2, \dots, x_n)$, er dens gradient givet: \begin{equation} \nabla f(x_1, x_2, \dots, x_n) = \begin{bmatrix} \frac{d}{dx_1} f(x_1, x_2, \dots, x_n)\\ \frac{d}{dx_2} f(x_1, x_2, \dots, x_n)\\ \vdots \\ \frac{d}{dx_n} f(x_1, x_2, \dots, x_n)\\ \end{bmatrix} \end{equation}

For at definere Gradient descent algoritmen har vi brug for en notation der angiver hvor mange skridt vi allerede har taget. Vi angiver punktet efter $s$ skridt som: $x_1^{(s)}, x_2^{(s)}, \dots, x_n^{(s)}$. I gradient descent algoritmen vælger man et startpunkt $x_1^{(0)}, x_2^{(0)}, \dots, x_n^{(0)}$ og derefter tager man skridt på følgende måde indtil: \begin{equation} \begin{bmatrix} x_1^{(s+1)}\\ x_2^{(s+1)}\\ \vdots\\ x_n^{(s+1)} \end{bmatrix} = \begin{bmatrix} x_1^{(s)}\\ x_2^{(s)}\\ \vdots\\ x_n^{(s)} \end{bmatrix} - \gamma \nabla f(x_1^{(s)}, x_2^{(s)}, \dots, x_n^{(s)}), \end{equation} hvor $\gamma$ er en konstant der angiver skridtlængden og gradienten er evalueret i det nuværende punkt. Man bliver ved med at tage skridt indtil gradienten er meget tæt på nul, fordi så har man nået et minimum. Prøv at studér [6] nærmere for at lære mere om Gradient Descent metoden.

I din SPR kan du vise, hvordan man anvender Gradient Descent til at minimere simple problemer. Prøv fx med andengradspolynomier med 1 og 2 variable, det kunne være:

  1. $f(x) = 2x^2 - 3x + 1$
  2. $f(x_1, x_2) = 3x_1^2 + 2x_2^2$

Du kan plotte funktionerne sammen med hvert skridt Gradient Descent algoritmen tager. Du kan også undersøge effekten af forskellige værdier af $\gamma$.

Sidst men ikke mindst, kan du også forsøge at anvende Gradient Descent til at beregne mindste kvadraters metode for vores talpuslepil.

Litteratur